zadanko hundayd: W trójkącie prostokątnym ABC długość przyprostokątnej AC stanowi 75% długości przyprostokątnej BC. Przez wierzchołek C poprowadzono prostą która przecina bok AB w takim punkcie D, że trójkąty ACD i BCD mają takie same obowdy. Znajdźstosunek długości promieni okręgów wpisanych w trójkąty ACD i BCD.

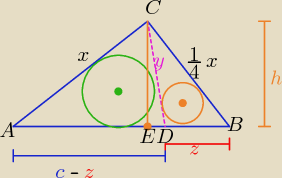
hundayd: Ma ktoś może pomysł !? Pomyślałam,żeby odcinek AC w tym trójkacie to jest 1/4 x , gdzie x to długość AC. Dobrze rozumuje?

malibur: o kurcze, nie wiem:(

Eta: Moja odp to:

r(ΔACD)		15−3√17
	=
r(ΔBCD)		2

malibur: ale jak do tego doszłaś?:(

Eta:

	1
x>0 |AC|=x |BC|=		x
	4

	1		17		√17
|AB|2= c2= x2+		x2 =		x2 ⇒ c=		x
	16		16		4

z porównania obwodów Δ ADC i BDC mamy:

	1		3+√17
x+y+c−z=		x+y+z ⇒ 2z= ............. =		x
	4		4

trójkąty ADC i BDC mają wspólną wysokość h to pola tych trójkątów są :

	|AD|*h		|DB|*h
P(ΔADC)=		P(ΔBDC)=
	2		2

	r ( okręgu zielonego)		P(ΔADC)
		=		=..........
	r (okręgu brązowego)		P(ΔBDC)

dokończ ..............

rumpek:

Eta:

Eta: Troszkę "parszywe" rachunki